#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, m;
cin >> n;
int cnt = 0;
while (n)
{
if(n % 2 == 0) break;
else
{
n /= 10;
}
cnt ++ ;
}
cout << cnt;
return 0;
}
#include <stdio.h>
int main()
{
int n, m;
scanf("%d", &n);
int cnt = 0;
while (n)
{
if(n % 2 == 0) break;
else
{
n /= 10;
}
cnt ++ ;
}
printf("%d", cnt);
return 0;
}
B
题意
n个正整数,可以将一些数放入背包,需要使得背包中的数的总和为偶数且为最大值。
解题思路
我们可以将所有的数放入背包,如果此时总和为偶数,那么这就是满足条件的数。
如果此时总和为奇数,那么我们只需要把最小的一个奇数拿出去,那么总数就变成了偶数,也就是满足条件的最大值。
c++代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int a[N];
int main()
{
cin >> n;
int sum = 0;
for (int i = 0; i < n; i ++ ) cin >> a[i], sum += a[i];
// sort排序函数,默认从小到达排序
sort(a, a + n);
for (int i = 0; i < n; i ++ )
{
// 总和为偶数,直接跳出循环
if (sum % 2 == 0) break;
// 总和为奇数,找到最小的奇数
else if (a[i] % 2 == 1)
{
sum -= a[i];
break;
}
}
cout << sum << endl;
return 0;
}
c代码
#include <stdio.h>
#include <math.h>
const int N = 1e5 + 10;
int a[N];
int main()
{
int n;
scanf("%d", &n);
// sum为总和
int sum = 0;
for (int i = 0; i < n; i ++ )
{
scanf("%d", &a[i]);
sum += a[i];
}
//如果为奇数,就去掉最小的那个奇数
if (sum % 2 == 1)
{
int mi = 1e9;
for (int i = 0; i < n; i ++ )
if (a[i] % 2 == 1) mi = mi < a[i] ? mi : a[i];
sum -= mi;
}
printf("%d", sum);
return 0;
}
C
题意
题意就是求$mex(a_1,…a_r) * gcd(a_1…a_r)$的最大值
其中$a_1…a_r$可以是任意连续区间
gcd就是求最大公约数,而mex求的是区间中未出现的最小非负整数
例如 mex(0,2,3)=1
解题思路
我们其实可以发现,如果区间里没有0的话,那么mex()的值为0,就一定不是最大值了。
所以我们需要从包含0的区间入手。
而这又分为两种情况,包含1,和不包含1
当区间不包含1时,mex()的值就一定是1,此时就需要保证gcd()的值最大
当区间包含1时,gcd()的值就一定是1,此时就需要保证mex()的值最大
综上所述,我们需要找到包含0的区间内,gcd()的最大值,和mex()的最大值
当我们以0为起始点,向左或向右走一步,此时gcd()就是最大值。因为加入更多的数后,最大公约数,只会不变或减小,而不可能增加。
而mex()的最大值就是包含所有n个数。因为mex()求的是最小的没有出现过的正整数,包含的数越多,mex()的值只会不变或增加,而不会减小。
需要注意的是,当所有数都为0的时候,要进行特判。
c++代码
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;
const int N = 1e5 + 10;
typedef long long ll;
int n, m;
int a[N];
int c[N]; //存储每个数出现的次数
int main()
{
cin >> n;
ll sum = 0;
for (int i = 0; i < n; i ++ )
{
cin >> a[i];
sum += (ll)a[i];
c[a[i]] ++ ;
}
// 当所有数都为0,直接输出0
if (sum == 0)
{
cout << 0;
return 0;
}
int res = 0;
// mex()的最大值
while (c[res]) res ++ ;
for (int i = 0; i < n; i ++ )
{
if (a[i] == 0)
{
// 防止越界,需要特判i的值
if (i > 0) res = max(res, a[i - 1]);
if (i < n) res = max(res, a[i + 1]);
}
}
cout << res << endl;
return 0;
}
c代码
#include <stdio.h>
const int N = 1e5 + 10;
int a[N];
int c[N]; //存储每个数出现的次数
int max(int a, int b)
{
if (a > b) return a;
else return b;
}
int main()
{
int n;
scanf("%d", &n);
int sum = 0;
for (int i = 0; i < n; i ++ )
{
scanf("%d", &a[i]);
sum += a[i];
c[a[i]] ++ ;
}
// 当所有数都为0,直接输出0
if (sum == 0)
{
printf("%d", 0);
return 0;
}
int res = 0;
while (c[res]) res ++ ;
for (int i = 0; i < n; i ++ )
{
if (a[i] == 0)
{
// 防止越界,需要特判i的值
if (i > 0) res = max(res, a[i - 1]);
if (i < n) res = max(res, a[i + 1]);
}
}
printf("%d\n", res);
return 0;
}
D
题意
有t波丧尸,有两种武器,一种发射一枚子弹,另一种向所有的僵尸发射一枚子弹。
而丧尸被击中后不会死掉,且会复制一个新的丧尸,当丧尸数量是 $2^{20}$的倍数的时候,丧尸可以被消灭。
解题思路
首先子弹数量非常充足,一定可以消灭丧尸(一个个的加也可以到$2^{20}$)
对于$2^{20}$,我们可以转化为2进制来看,1000……,丧尸的数量同理也转化为2进制,如10111
要成为1000……这种数字的倍数,需要保证自身二进制下的最后一个1在1000…..中1的位置或靠左的位置,如1000,那么101000就是他的倍数
问题也就转化为了将n的二进制表示下最后一个1移动到$2^{20}$的二进制下1的位置或靠左的位置。
武器一每次会让丧尸的数量增加1,武器二每次会让丧尸的数量$*$2,也就是在二进制下的数左移一位(即在末尾加一个0)
所以最多需要射击的次数是20,也就是每次都使用武器二的情况。
所以只需要枚举20次,每次多使用一次武器一,取最少的次数即可。
c ++代码
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;
int main()
{
int t;
cin >> t;
while (t -- )
{
int n;
cin >> n;
int res = 20;
for (int i = 0; i < 22; i ++ )
{
int m = n;
int cnt = 0;
//cnt为n的最右边的1的位置
while (m % 2 == 0)
{
m >>= 1;
cnt ++ ;
}
res = min(res, i + max((20 - cnt), 0));
n ++ ;
}
cout << res << endl;
}
return 0;
}
c代码
#include <stdio.h>
int min(int a, int b)
{
if (a < b) return a;
else return b;
}
int max(int a, int b)
{
if (a > b) return a;
else return b;
}
int main()
{
int t;
scanf("%d", &t);
while (t -- )
{
int n;
scanf("%d", &n);
int res = 20;
for (int i = 0; i < 22; i ++ )
{
int m = n;
int cnt = 0;
//cnt为n的最右边的1的位置
while (m % 2 == 0)
{
m >>= 1;
cnt ++ ;
}
res = min(res, i + max((20 - cnt), 0));
n ++ ;
}
printf("%d\n", res);
}
return 0;
}
E
题意
一个密码,长度不定,只有6种字符,只要密码后缀是@qq.com这7个字符,就算输入成功。
每一秒随机输入一位,输入错误就重新输入,直到正确。现在需要求出期望时间的个位数。
然后还有一个道具每使用一次可以是期望时间x变为$x^2$。
解题思路
一种特殊情况就是,密码长度小于7,那么永远都无法输入正确,时间也就趋于正无穷,输出-1.
每次输入正确的概率是$\frac{1}{6^7}$,期望概率P=$6^7$,那么期望时间就是np=$n*{6^7}$
${np^2}^{m}$(就是np的2次方的m次方)
这道题的核心是个位的变化,下面是个位的数字在平方之后的变化,不难看出,在平方两次之后,个位的数字是不再变化了的,所以我们不用去真正的循环m次,最多只需要循环两次,就可以算出期望数的个位。而且m的范围是1e9,直接枚举是铁定超时的。
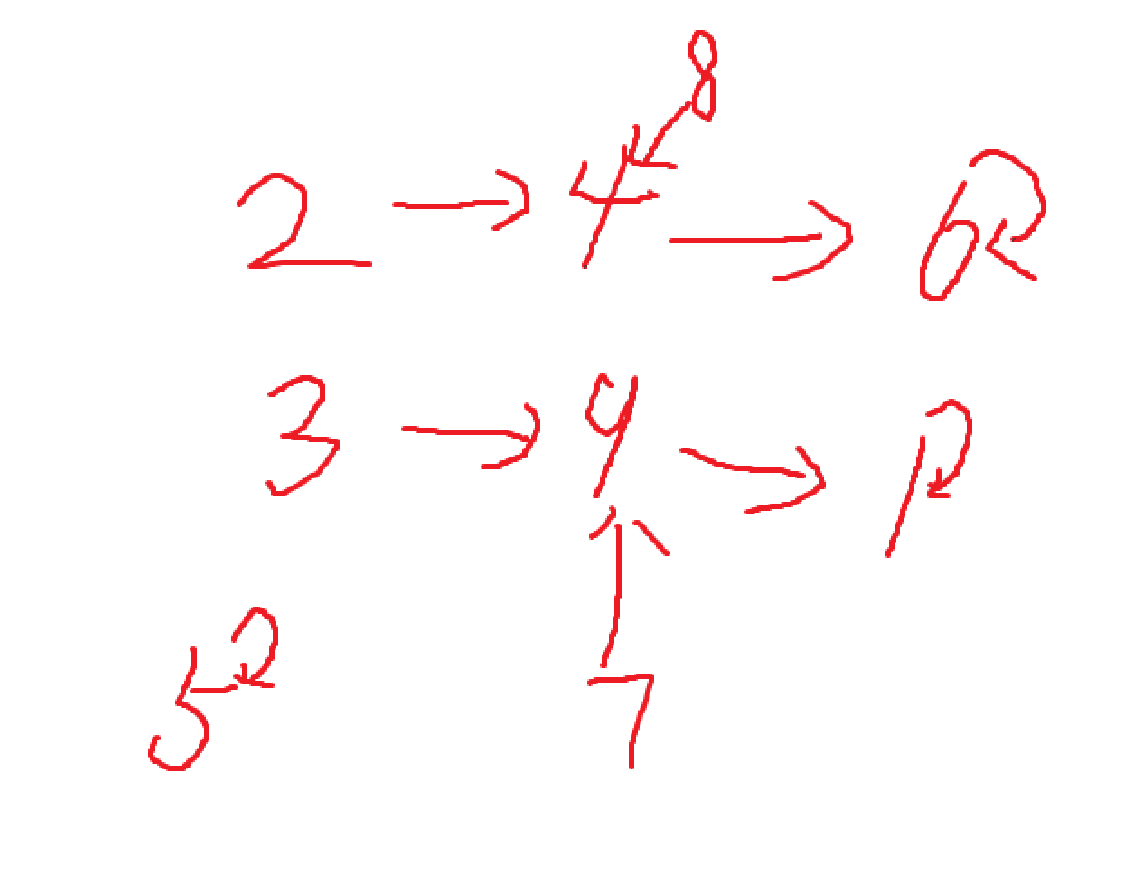
c++代码
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;
int main()
{
int n, m;
cin >> n >> m;
// 如果n<7,无法解开
if (n < 7)
{
cout << -1;
return;
}
// 我把6^7给省略了,因为实际上只用得到他各位的6,n同样也只用到个位数
n %= 10;
// 原始期望时间
int res = n * 6 % 10;
// 使用道具之后
m = min(2, m);
while (m -- ) res = res * res % 10;
cout << res;
return 0;
}
c代码
#include <stdio.h>
int min(int a, int b)
{
if (a > b) return b;
else return a;
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
// 如果n<7,无法解开
if (n < 7)
{
printf("%d", -1);
return 0;
}
// 我把6^7给省略了,因为实际上只用得到他各位的6,n同样也只用到个位数
n %= 10;
// 原始期望时间
int res = n * 6 % 10;
// 使用道具之后
m = min(2, m);
while (m -- ) res = res * res % 10;
printf("%d", res);
return 0;
}



